This is the second installment of "Major Component Lifecycle Improvement Case Study, Part I." Read the first part this case study here.
Replacement Strategy. Minimization of Downtime.
Once the curves that identify the component are obtained, a model is intended to be used to determine the optimum replacement age of valve housing while minimizing the downtime per unit of time.
There are two probable operating intervals that valve housing can show: first, when the component will reach the optimum replacement age; and when to cease functions due to a failure before reaching the desired age. In each case the replacement interval is different. While one is a programmed period, the other corresponds to an unforeseen event period.
This model also assumes:
- There are no fixed intervals of preventive replacements, meaning the replacement time is determined by the age of an item and not a fixed period from the last replacement order.
- When a failure occurs, a replacement is made.
- When a failure occurs, the age of the new item is set to zero.
Based on this model, there are two cycles of operation that an item can have: the first is when the item arrives at the optimum age for replacement, and the other is determined by the termination of service due to a failure occurred before reaching at this age.
The total downtime per unit time is expressed as:
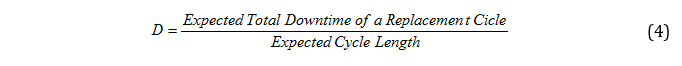
The Expected Total Downtime of a replacement cycle is equal to the downtime due to a preventive replacement multiplied the probability of occurrence of this event, plus the downtime due to a failure multiplied the probability of occurrence of one:
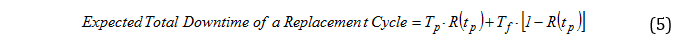
On the other hand, the expected length of a cycle can be understood as the period of preventive replacement multiplied the probability of occurrence of the same, plus the expected period for a failure multiplied the probability of occurrence in such a period.
The expected period for a failure can be interpreted as the mean time between failure for a course from scratch and the period of preventive replacement.
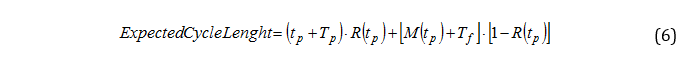
And
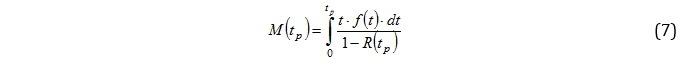
Replacing 5, 6 and 7 into 4, we obtain the equation that rules the model:
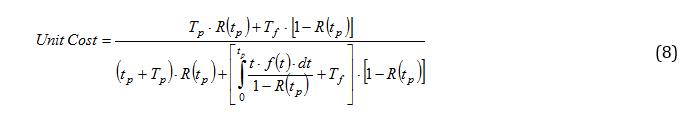
Figure 5 shows the same equation for different cost relationships between failure and preventive replacements.
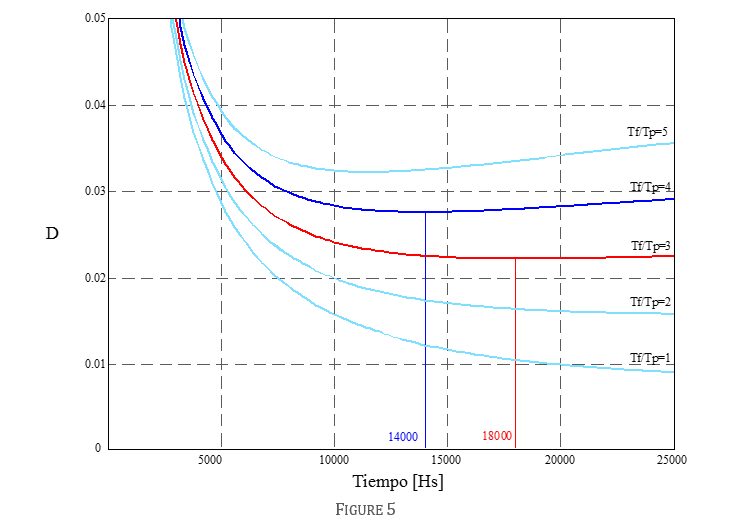 As can be seen for a ratio of 3, the lost time finds its minimum at 18,000 hours, and at four this minimum is reached at 14,000 hours.
As can be seen for a ratio of 3, the lost time finds its minimum at 18,000 hours, and at four this minimum is reached at 14,000 hours.
Results and Discussion
According to the probabilistic analysis, the replacement time was set at a minimum of 16,000 hours. Additionally monthly inspections to measure wear were established.
Two following records corroborated the probabilistic model. In those cases, it was decided to run to failure in order to know how much it could last: the first failure occurred in the valve housing #3 after 16,034 operating hour. Almost a month later, the second expected failure occurred. In this case, again in valve housing #3 after 18,500 operating hours.
Although the probabilistic model is quite accurate, it doesn’t point to the ideal failure mechanism itself.
The shown failures consisted of a prick that communicates with the stud orifice letting the high pressure copper concentrate reach the exterior. These failures are far from what was expected analyzing the FEA model as correct mounted suction valve housing should fail from fatigue in the valve seat contact area (See the Valve Housing Stress Spectrum (diagonal section) under, Second Model, Page 6).
This analysis supposes that something else can be done under the CI way.
Further studies
Following the carried out analysis, we have acquired a solid base of knowledge. It leaves us in conditions to face and approach new limits for the component.
Valve Housing Material
The Manufacture Standards Manual establishes that the housings are manufactured from a 25CrMo4 / SAE 4130 steel with quenching and tempering heat treatment.
This steel has been widely employed since the 30’s, and is still one of the most widely used low-grade alloy steels because of its combinations of weldability, ease of fabrication, and mild hardenability from heat treatment. Although, it needs surface finishing for corrosion protection and it is very susceptible to hydrogen embrittlement (present in aqueous environments).
A thesis studying the dependence of strength on corrosion-fatigue resistance of 4130 steel, showed that decreases in fatigue life caused by the corrosive environment ranged from 100% in the lowest strength level to 190% in the higher strength levels. This result showed that higher strength in this steel corresponds to increasing detriment to fatigue life when exposed to an aqueous salt environment.
Even though this steel is considered proper for being applied in pressure vessel, an aqueous-corrosive environment results harmful. An inner metal sheathing is necessary for these components, preferably weldable, just to avoid detachments.
Metal Sheathing
Is it clear that the product must combine excellent properties of wear resistance and corrosion. For these purposes cobalt alloys are the most successful and effective known sheathings. They join the desired properties also at high temperatures.
This range highlights the Stellite® alloys that are mostly cobalt based and added with Cr, C, W and/or Mo. They are resistant to cavitation, corrosion, erosion and abrasion. The Stellite alloys retain their properties at high temperatures where they also have excellent oxidation resistance. They can be finished to exceptional levels of surface finish with a low coefficient of friction to give good sliding wear.
Specifically Stellite® 6 is the most popular alloy as it provides a good balance of all of these properties.
Implementation
The financial statement allowed us to pass to the next stage and develop the application technology.
Once determined the hardfacing areas, an application procedure was developed, since this electrode need parts preheating.
The follow sequence shows the execution and the final product.
Final Results
After 4000 operating hours (1/4 of the expected life of an untreated valve housing), the test housings did not show any wear inside.

Nomenclature
Cp, scheduled replacement cost
Cf, failure replacement cost
f(t), failure probability distribution function
H(t), risk function
M(tp), mean time between failure in a period [0,tp]
R(tp), Reliability function
t, time
tp, replacement period
References
Andrew Kennedy Skilling Jardine, Alberth. C. Sang (2005). “Maintenance, Replacement And Reliability. Theory and Applications”
Charles E. Ebelin (2005). “An Introduction To Reliability And Maintainability Engineering”